Long Division Method for Cube Root by Peethanis

Cube Root

If any number x is multiplied itself three times, the result is called x cube.

x*x*x = x³                                    _

There fore x = Cube Root of x³ = ³√x³

Please find the below table for the Cubes of 1 to 9.

Here we can notice, Cube of 3 ends with 7, 4 ends with 4, 5 ends with 5, 6 ends with 6, 7 ends with 3, 8 ends with 2 and 9 ends with 9.

Perfect Cube: 1, 8, 27, 64, 125, 216, 343, 512, 729, ..... are called Perfect Cubes whose Cube Roots are exact numbers.  Any Real number multiplied itself three times, the cube is called Perfect Cube.

Easy Method for finding out Cube Roots for Perfect Cube:

Example 1: To find out Cube Root of 421875.

Solution:  By grouping each 3 digits from right to left of 421875 is 421'875.

               Now take the 1st group from left, which is 421 guess the which cube is maximum and less than or equal to 421. We can guess 7, as the cube of 7 is 343 will satisfy the condition.  And next group  from left is 875, ending with 5 means cube of 5.

                                                         

   So, the Cube Root is 75.

Long Division Method:

                                                                       _____
To find out Cube Root of 15625:     Denoted by ³√15625

Long Division Method:         Set up a division with the number, with grouping each 3 digits from the decimal point to left.

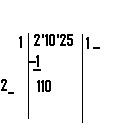
Take the 1 st group from left side, which is 15 as new dividend.  Check which cube is the maximum and less than equal to 15.  3³ is 27 which is more than 15.  So 2³ will satisfy the condition.  Now place 2 right sides, and 2³=8 below 15.  Subtract 8 from 15, remainder is 7.

Bring down next group 625, and place after 7.  So the new dividend is 7625.  Now place  _² + 30*2(10*2 _) left side as new divisor where 2 is initial quotient, blank is for new quotient and place a blank  on right side after 2.

Guess a new quotient to fill in the blanks of the new divisor and quotient such that   the product of new quotient and new divisor should be maximum and less than equal to 7625.

We can estimate new quotient from the formula :    380*estimate*2² = present dividend

                                                                                                        where 2 is initial quotient

                                                                                                        1520*estimate=7625

                                                                                                        estimate= 7625/1520 = ~ 5                                                                                                                                                                                 

                                                                            Choose 5 as the new quotient, and fill the blanks.

New divisor is  5² + 30*2(10*2 +5) = 25 + 1500 = 1525

Then the product = 1525 * 5 = 7625

Place 7625 below 7625, and subtract. The remainder will be "0". The quotient is 25.

Explanation:

Let ab, a two digit number be the Cube Root of a given number C.

In ab, a is in Tenth place and b is in Units.

The value of ab is 10*a + b.

   _

³√C = 10*a + b

cubing both sides

C = (10*a + b)³

C= 1000*a³ + 3*10*a*b*(10*a + b) + b³

C-1000*a³ =  3*10*a*b*(10*a + b) + b³

C-1000*a³ =  30*a*b*(10*a + b) + b³

C-1000*a³ =  (30*a*(10*a + b) + b²) * b
LHS is C-1000*a³ which is nothing but remainder after performing with the quotient a.
RHS is (30*a*(10*a + b) + b²) * b which is nothing but the product of new divisor 30*a*(10*a + b) + b² and new quotient b.

We can also write 30*a*(10*a+b) +b²  as 30*a* ab +b² where ab is not a*b.

In each operation, if the new quotient is b then the new divisor will be 30*a*(10*a + b) + b² where a is initial quotient.

Long division method for Square Root by Peethanis

Long Division Method 

For finding out Square Root: 

                                                                                                            

To find out Square root of a number 21025:
                           _____
It is denoted by √21025

Long Division Method:

Set up a division with the number 21025 and by grouping each 2 digits of the dividend 21025 from right to left, we can rewrite as  2'10'25.  Starting from 1st group from left most, which is 2,  guess which square is maximum and  less than or equal to 2. Because 1² is less than 2, we can choose 1  as the quotient, and divisor. Place 1 on the right side and  left side. Place  1²=1 below 2. Subtract 1 from 2, the remainder is 1.

Bring down next group 10, place it after 1. Now the new dividend will become 110.  Place double of the quotient which is 1x2=2 on left side as the new divisor and  reserve a room  right side of  it and the quotient.                                                   

                                                         

Now guess  a new quotient  which is suitable to fill in both the blanks, such that the product of the new quotient and new divisor should be maximum and less than or equal to 110.  Select  4 as the new quotient and place in the blanks. Now place the product of the new divisor and new quotient is 24*4 = 96 below 110, subtract it from 110, the remainder will be 14.

                                                         

                                                                

Bring down the next group 25, place it after 14, then the new dividend is 1425.  Now place double of the quotient means 28 on left side as new divisor and put a blank after it  and the quotient 14.

                                                           

We can estimate the new quotient from the formula 20*old quotient*estimate= present dividend.
                                                       20*14*estimate=1425
                                                       estimate=1425/280=5.089

So we can choose 5 as a new quotient, such that the product of 285 and 5 is maximum and less than or equal to 1425.  Put 5 in both the blanks and place the product 285*5 =1425 below 1425 and subtract.  The remainder is "0".

                                                                   

                                                  _____
So, the quotient is 145 which is √21025.

Explanation:

                                                     

Let ab, a two digit number be the square root of  a given number C.
                                           __
                                         √C   = ab

 In ab, a is in Tenth place and b is in Units place.

The value of "ab" is 10 times a, plus b.  ie.10*a + b.

                                        __

                                      √C   = 10*a + b 

                                      Squaring both sides

                                      C = (10*a + b)²

                                      C =100* a²+ b²+20*a*b

                                      C-100*a² = b² + 20*a*b
                                      rewriting the above

                                      C-100*a² = (20*a + b)*b

LHS =C-100*a²  is nothing but the remainder after performing  with initial quotient a.

RHS=b*(b+20*a) is nothing but the product of new quotient b and new divisor (20*a + b).

Here 20*a + b  means double of a in Tenths place and b in Units place which can be denoted by (2*a)b

In the above example a=1 and b=4, so 20*a +b=24 which is nothing but 4 placed after the double of 1.

And in the next step, a=14 and b=5, so 20*a +b=285 which is nothing but 5 placed after double of 14.

Like this in each operation, we have to choose a new quotient b, such that product of new divisor(20*a +b) and new quotient (b) should be maximum and less than or equal to the new dividend.